Many investors prefer investing their savings in bonds, which can offer steady income with relatively lower risk than stocks. In 2022 and 2023, bond yields rose while yield curves flattened and then inverted. This pushed many investors to buy short-term debt instruments, like treasury bills. However, now that bond yields have peaked and central banks are starting to lower interest rates, investors in short-term bonds face reinvestment risk. This means that when their bonds mature, they might have to reinvest their capital at lower yields. As yield curves start to steepen again, investing in longer-term bonds may become an attractive strategy. But this also increases interest rate risk, especially if inflation does not behave as expected and central banks do not fully deliver the interest rate cuts that are currently being anticipated by the market. This article aims to simplify some of the more intricate concepts related to bonds, focusing on the critical role of bond convexity and how this can be used to the advantage of investors as they reposition their portfolios in the current climate.
Bond Yields and Duration
Let’s start with the basics. Bond prices and yields move in opposite directions. When interest rates rise, bond prices fall, and when rates drop, bond prices go up. This happens because bonds pay a fixed coupon (interest payment). For example, if you own a bond with a 5% coupon and new bonds are issued with a 6% coupon, your bond becomes less attractive, and its price will drop to offer a comparable yield to the new bonds. This is a fundamental principle in bond investing.
Duration is a key measure of how sensitive a bond’s price is to interest rate changes. It estimates how much a bond’s price will change if interest rates rise or fall by 1%. For instance, if a bond has a duration of 5, a 1% increase in rates would lower its price by about 5%, and a 1% decrease would raise its price by about 5%.
While duration is an essential concept for understanding and managing interest rate risk, it has limitations, particularly when interest rates change significantly. This is where convexity comes in.
Why Investors Love Bond Convexity
Convexity gives a more accurate picture of how bond prices respond to interest rate changes, especially when those changes are large. Unlike duration, which assumes a linear relationship between a bond’s price and its yield, convexity accounts for the fact that the duration itself changes as interest rates change, leading to a curved relationship between bond prices and yields. For the mathematically inclined, convexity is the second derivative of a bond’s price with respect to interest rates. Conceptually, it measures the degree of the curvature in the price-yield relationship.
In more simple and practical terms, bonds with higher convexity will rise more in price when rates fall and lose less when rates rise, compared to bonds with lower convexity. This is great news for investors!
Convexity is a desirable property for investors because it enhances the benefits of duration when bond prices are rising, and it cushions against losses when interest rates are volatile. Let’s look at an example using German government bonds with different tenors. We will assume the same amount of money is invested in each bond and show how much an investor might earn over one year in two scenarios: if interest rates rise by 1% or if they fall by 1%.
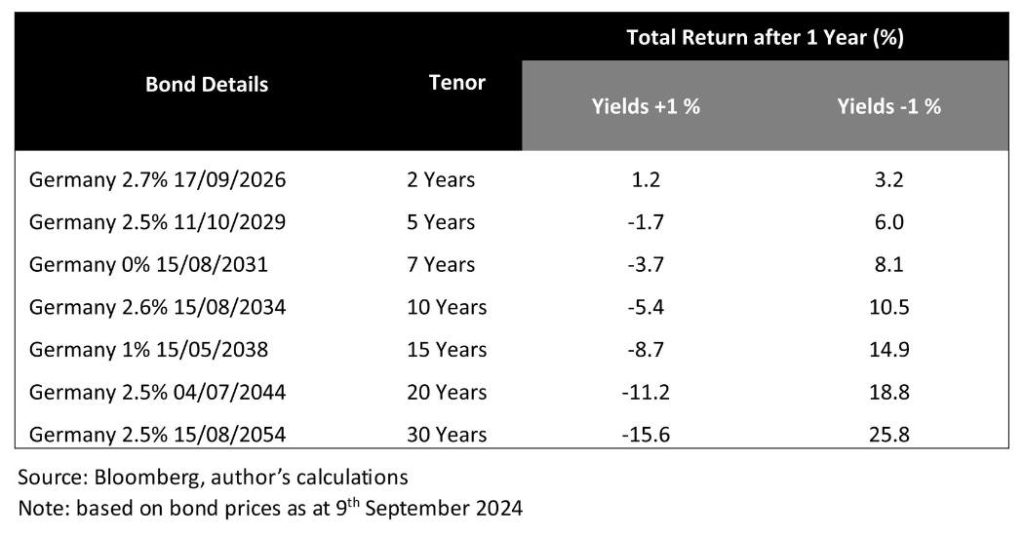
As you can see, longer-term bonds exhibit significantly higher volatility in response to interest rate changes. Notably, even in an adverse interest rate environment, the two-year bond can still generate a positive total return over a one-year period. This occurs because the coupon income compensates for the limited capital losses, given that shorter-dated bonds are less sensitive to interest rate movements.
However, the key takeaway from this example is that the positive returns when yields fall are considerably larger than the losses when yields rise. This phenomenon occurs because of the bond convexity, and it underscores the importance of understanding both convexity and duration when investing in bonds.
Not All Bonds Are The Same
Convexity varies from bond to bond and it is not constant for each individual bond. Without delving into unnecessary detail, a bond convexity is influenced by several factors including its coupon rate, time to maturity, and yield.
More importantly, while convexity generally works in favour of investors, it can have the opposite effect when a bond has an embedded call option. A callable bond allows the issuer to redeem the bond before its maturity date, typically when interest rates fall. This feature alters the bond convexity.
Callable bonds exhibit negative convexity at certain interest rate levels. When interest rates fall, the bond’s price increases, but not as much as it would for a non-callable bond. This is because the likelihood of the issuer repaying the bond early increases, capping the bond’s price appreciation. Investors, anticipating the early call, will not bid up the price as much, leading to lower price gains compared to bonds without call options.
Bond Convexity: Final Thoughts
Understanding bond convexity is crucial for bond investors. As we transition to a period of lower interest rates, investors might consider purchasing longer-duration bonds to mitigate reinvestment risk in the coming years. By doing so, investors would increase their portfolio’s sensitivity to interest rate changes. While it is likely that yields will continue to trend downward over the coming quarters, this outcome is not guaranteed. In such eventuality, investors can take comfort in knowing that bond convexity will help cushion their downside risk!

Written by
David Lanzon, CFA
Senior Portfolio Manager, ReAPS Asset Management Ltd
The information contained in this article represents the opinion of the contributor and is solely provided for information purposes. It is not to be interpreted as investment advice, or to be used or considered as an offer, or a solicitation to sell / buy or subscribe for any financial instruments nor to constitute any advice or recommendation with respect to such financial instruments. This article was issued by ReAPS Asset Management Limited, a subsidiary of APS Bank plc. ReAPS Asset Management Limited (C77747) with registered address at APS Centre, Tower Street, Birkirkara BKR 4012 is regulated by the Malta Financial Services Authority as a UCITS Management Company and to carry out Investment Services activities under the Investment Services Act 1994 and is registered as an Investment Manager under the Retirement Pensions Act.


